Аналіз обсягів бюджетного відшкодування податку з доходів фізичних осіб за допомогою багатофакторної регресійної моделі

Для побудови вказаної багатофакторної регресійної моделі використовується матриця вихідних даних, елементами якої є значення сум ПДФО, повернених у зв’язку з нарахуванням податкового кредиту, та сум сплаченого ПДФО, сум витрат, що входять до податкового кредиту, та кількості платників в розрахунку за кожний місяць 2006-2007 рр. ДПІ в Київському р-ні м. Харкова (Додаток Б) [11, 12].

За допомогою пакету статистичних методів STATISTICA 6.0 отримаємо результати багатофакторної регресійної моделі (рис. 2.12).

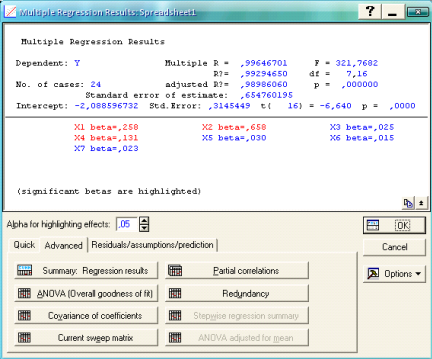
Рис. 2.12 Результати багатофакторної регресійної моделі

Значення коефіцієнту множинної кореляції Multiple R = 0,9965 свідчить про те, що між залежною змінною та всіма незалежними факторами існує достатньо тісний зв'язок. Значення коефіцієнту детермінації R2 = 0,9929 свідчить про те, що варіація суми ПДФО, поверненої з бюджету у зв'язку з нарахуванням податкового кредиту, на 99,3% залежить від факторів, які були відібрані для побудови регресійної моделі. Це означає, що вибрані фактори оказують істотний вплив на залежну змінну.

Проведемо аналіз адекватності побудованої моделі на основі критерію Фішера (F - критерію). Розраховане значення F - критерію складає 321,768, що перевищує табличне значення Fтабл = 2,25, оскільки p < 0,05. Це підтверджує адекватність побудованої моделі та істотність кореляційного зв'язку між досліджуваними параметрами моделі.

В моделі існує чотири фактори, які несуттєво впливають на залежну змінну - це фактори Х3, Х5, Х6, Х7 (сума витрат на сплату процентів з іпотечного кредитування, недержавне пенсійне страхування та довгострокове страхування життя, штучне запліднення чи всиновлення дитини, благодійну допомогу, що входять до податкового кредиту). Для кожного параметру моделі проаналізуємо значення критерію Стьюдента, за допомогою якого визначають статистичну значимість параметрів (рис. 2.13).

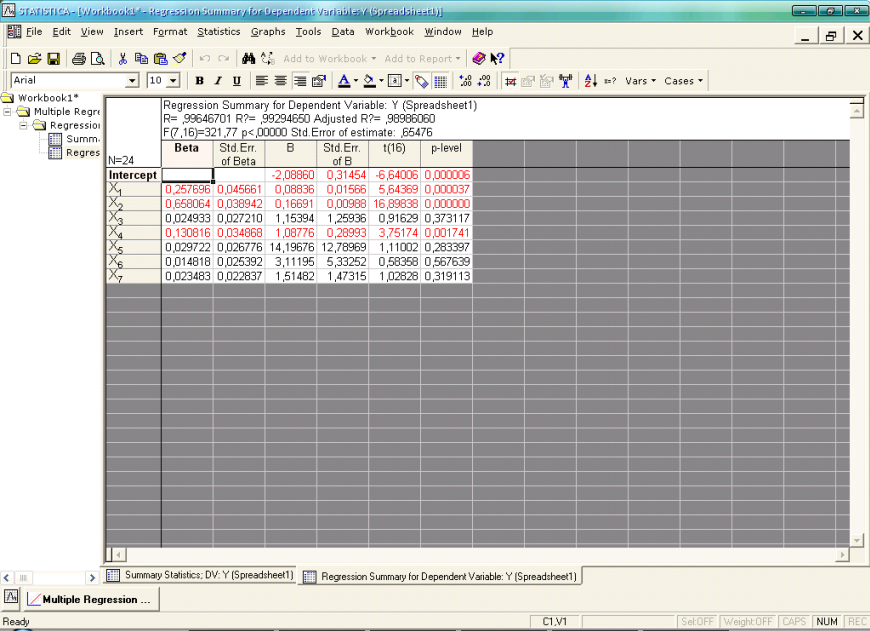
Рис. 2.13 Результати побудованої багатофакторної моделі

За допомогою критерію Стьюдента з ймовірністю 95% можна сказати, що фактори Х1, Х2, Х4 є значими для побудованої моделі, оскільки їх розрахункові значення t > tтабл (tтабл (16) = 2,119). Так, для факторів Х3, Х5, Х6, Х7 розрахункові значення критерію Стьюдента t не перевищують tтабл, оскільки для них значення p > 0,05. Це свідчить про те, що ці параметри моделі не є значимими.

При отриманих результатах модель буде мати наступний вигляд:

= - 2,089 + 0,088X1 + 0,167X2 + 1,154X3 + 1,088X4 +

+ 14,197X5 + 3,112X6 + 1,515X7

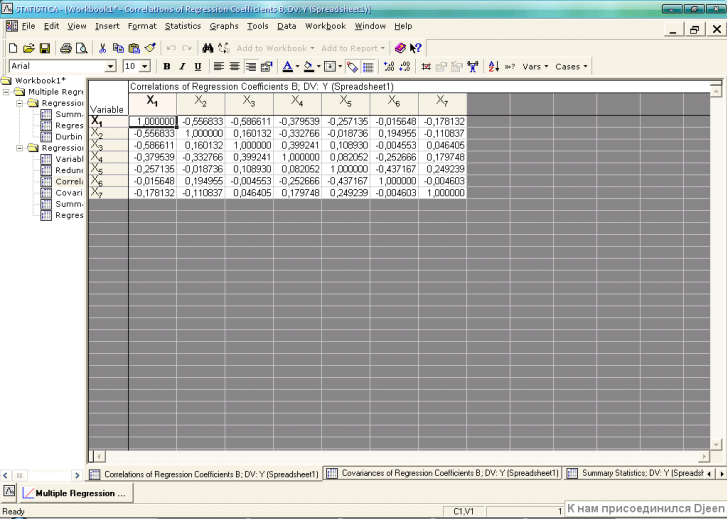
Перевіримо адекватність моделі за допомогою матриці парних кореляцій (рис. 2.14). Коефіцієнти парних кореляцій показують взаємозв’язок між парами факторів та змінюються від -1 до 1 (чим ближче значення до 1, тим сильніший взаємозв’язок між факторами). Наявність кореляції між незалежними змінними свідчить про неадекватність моделі.

Читайте більше

Фінансовий аналіз діяльності ВАТ Завод ім. Фрунзе
Фінансовий аналіз - це дослідження фінансового стану й основних результатів фінансової діяльності підприємства з метою виявлення резервів подальшого підвищення його ринкової вартості й забезпечення ефективного розвитку. Проведення фінансового аналізу є актуальним для кожного підприємст ...

Основні напрямки реалізації видатків державного бюджету України
Бюджет та бюджетна система загалом відноситься до тієї сфери суспільного життя, що безпосередньо стосується інтересів всіх і кожного. В бюджеті будь-якої країни відбиваються важливі економічні, соціальні, політичні проблеми життя суспільства і людини. Актуальність обраної для дослід ...